Video pembelajaran Kubus dan Balok
Berbagai video dibawah ini akan membantu untuk lebih memahami materi kubus dan balok, silahkan klik setiap link yang diberikan dan selamat menikmati setiap video dan materi yang diberikan.
Tugas II : Jaring-jaring Kubus dan Balok
Lakukan kegiatan berikut bersama kelompok kalian !
Kubus
4. Apakah yang dapat kalian simpulkan dari jawaban-jawaban tersebut ?
5. Apakah pengertian jaring-jaring kubus menurut kalian ?
Balok
5. Apakah pengertian jaring-jaring balok menurut kalian ?


Kubus
- Carilah dua model kubus yang ukurannya sama yang terbuat dari bahan yang bisa digunting yang ada di sekitar kalian ( misalnya : kotak kue, kardus mie instan, kardus bekas tempat elektronik, dll ).
- Guntinglah model kubus I sepanjang tiga buah rusuk pada sisi atas dan empat buah rusuk pada sisi tegaknya.
- Rebahkan bidang-bidang hasil guntingan dari model kubus tersebut, sehingga diperolah rangkaian bangun datar yang kongruen.
- Untuk model kubus II, gunting sepanjang tiga buah rusuk pada sisi alas, satu buah rusuk pada sisi tegak,dan tiga buah rusuk pada sisi atas.
- Rebahkan bidang-bidang hasil guntingan dari model kubus II tersebut, sehingga diperolah rangkaian bangun datar yang kongruen.
- Bandingkan jaring-jaring kubus I dan jaring-jaring kubus II, samakah bentuk kedua jaring-jaring tersebut ?
- Gambarlah kedua jaring-jaring kubus tersebut !
- Menurut kalian dari keempat bangun pada gambar berikut ini jika dilipat menurut garis, bangun yang manakah yang dapat menjadi sebuah model kubus ?
4. Apakah yang dapat kalian simpulkan dari jawaban-jawaban tersebut ?
5. Apakah pengertian jaring-jaring kubus menurut kalian ?
Balok
- Carilah dua model balok yang ukurannya sama yang terbuat dari bahan yang bisa digunting yang ada di sekitar kalian ( misalnya : kotak kue, kardus mie instan, kardus bekas tempat elektronik, dll ).
- Guntinglah model balok I sepanjang tiga buah rusuk pada sisi atas dan empat buah rusuk pada sisi tegaknya.
- Rebahkan bidang-bidang hasil guntingan dari model balok tersebut, sehingga diperolah rangkaian bangun datar yang kongruen.
- Untuk model balok II, gunting sepanjang tiga buah rusuk pada sisi alas, satu buah rusuk pada sisi tegak,dan tiga buah rusuk pada sisi atas.
- Rebahkan bidang-bidang hasil guntingan dari model balok II tersebut, sehingga diperolah rangkaian bangun datar yang kongruen.
- Bandingkan jaring-jaring balok I dan jaring-jaring balok II, samakah bentuk kedua jaring-jaring tersebut ?
- Gambarlah kedua jaring-jaring balok tersebut !
- Menurut kalian dari keempat bangun pada gambar berikut ini jika dilipat menurut garis, bangun yang manakah yang dapat menjadi sebuah model kubus ?
5. Apakah pengertian jaring-jaring balok menurut kalian ?
Diagonal Bidang dan diagonal Ruang Kubus
a. Diagonal
bidang
Diagonal bidang adalah ruas garis yang
menghubungkan dua titik sudut yang berhadapan pada setiap sisi kubus
Diagonal
bidang kubus ABCDEFGH adalah :
AC,
BD, FH, GE, BE, AF, DG, CH, BG, CF, AH, DE
b. Diagonal
ruang
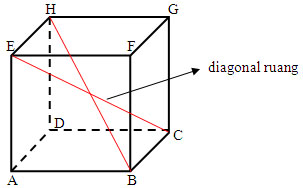
Diagonal
ruang adalah ruas garis yang menghubungkan dua titik sudut yang berhadapan
dalam suatu ruang kubus.
Diagonal
ruang kubus ABCDEFGH adalah : BH,
CE, AG, DF
c. Bidang
diagonal
Bidang
diagonal adalah bidang yang dibatasi oleh dua rusuk dan dua diagonal bidang
pada kubus.
BDHF, ACGF, ABGH, CDEF, ADGF,
BCHE
sumber : disini
Unsur-unsur Kubus
a. Sisi
kubus : bidang ABCD
bidang EFGH
bidang ABFE
bidang CDHG
bidang BCGF
bidang ADHE
b. Rusuk
kubus : AB, BC, CD, AD, AE, BF, CG, DH,
EF, FG, GH, EH
Rusuk-rusuk yang sejajar pada kubus :
AB//DC//EF //HG
AD// BC// FG//EH
AE//
BF//CG// DH
c. Titik
sudut : A, B, C, D, E, F, G, H
Unsur-unsur kubus lain seperti diagonal sisi, diagonal bidang dan diagonal ruang dibahas di sini
Tugas I : Identifikasi sifat-sifat kubus dan Balok
Lakukan kegiatan dibawah bersama dengan kelompokmu !
- Carilah model kubus dan balok dari karton.
- Buatlah ruas garis dengan spidol untuk menandai perpotongan dua buah persegi pada kubus
- Buatlah bulatan dengan spidol untuk menandai perpotongan tiga buah garis pada kubus .
- Setiap daerah persegi pada kubus disebut sisi kubus. Berapakah banyaknya sisi kubus ?
- Bandingkan bentuk dan ukuran semua sisi kubus. Apakah sama ? ( Jika sama, sisi-sisi kubus itu dinamakan kongruen )
- Perpotongan dua sisi kubus merupakan sebuah garis yang disebut rusuk kubus. Berapakah banyaknya rusuk kubus itu ?
- Bandingkan panjang semua rusuk kubus. Apakah ukurannya sama ?
- Titik perpotongan dari setiap tiga rusuk yang bertemu disebut titik sudut kubus. Berapakah banyaknya titik sudut kubus itu ?
- Apa yang dapat kalian simpulkan tentang kubus itu ?
- Sisi balok berbentuk apa dan berapa banyaknya ?
- Berapa banyaknya pasangan sisi balok yang berhadapan dan saling kongruen ?
- Berapakah banyaknya rusuk balok ?
- Bandingkan panjang semua rusuk balok. Apakah ukurannya sama ?
- Berapakah banyaknya titik sudut balok ?
- Apa yang dapat kalian simpulkan tentang balok itu ?
Mengenal Bidang, Rusuk dan Titik Sudut Kubus dan Balok
sumber : dari sini
Perhatikan ruang kelasmu !
a. Berbentuk bangun ruang apakah ruang kelasmu, balok atau kubus ?
b. Saat ini kalian berada pada bagian mana dari ruang kelas itu, bagian dalam atau bagian luar ?
c. Bagian dalam dan luar ruang kelasmu dibatasi oleh beberapa dinding, bukan ? Dinding itu merupakan batas yang memisahkan bagian dalam dan bagian luar ruang kelas. Berapa banyaknya dinding itu ? Bagaimanakah bentuknya ?
d. Apakah ruang kelasmu hanya dibatasi dinding-dinding saja ?
e. Apakah langit-langit dan lantai kelasmu merupakan batas ruang kelasmu ? Mengapa ?
f. Apakah langit-langit dan lantai merupakan bidang datar ?
g. Bila ruang kelasmu merupakan balok atau kubus, maka dinding serta langit-langit dan lantai ruang yang membatasi bagian dalam dan luar kelasmu dapat dipandang sebagai bidang. Berapa banyak bidang yang membatasi kubus dan balok ?
Perhatikan bahwa pada kubus dan balok terdapat bidang yang membatasi bagian dalam dan luar bangun ruang. Bidang yang demikian itu disebut bidang sisi dan untuk selanjutnya disebut sisi saja.
h. Perhatikan pertemuan ( perpotongan ) antara dinding dengan dinding, dinding dengan langit-langit dan dinding dengan lantai ruang kelasmu. Apakah yang terjadi ? Jelaskan !
i. Bila ruang kelasmu merupakan bangun kubus atau balok, dan dinding-dinding, langit-langit serta lantai ruang kelasmu merupakan sisi-sisinya, maka perpotongan sisi itu membentuk sebuah garis. Berapa banyak garis yang terjadi ? Garis tersebut dinamakan rusuk.
j. Perhatikan kembali ruang kelasmu yang merupakan kubus atau balok. Coba amati, adakah tiga rusuk yang berpotongan di satu titik ? Jika ada sebutkan dan berapa banyaknya ?
k. Pertemuan tiga atau lebih rusuk pada satu bangun ruang membentuk suatu titik.Titik yang demikian ini dinamakan titik sudut. Berikan contoh titik sudut pada ruang kelasmu !
|
Langganan:
Komentar (Atom)